数学者は分野の壁を超えた「言葉」を創り続ける

ヒトの脳が作り出す「イメージ」はどこまでも曖昧……。だから意味を定めるために「言葉」が生まれました。しかし、言葉をもってしても人と人のコミュニケーション、イメージの共有には常に困難がともないます。一つの言葉（単語）に対するイメージは人それぞれ、千差万別。正確なコミュニケーションのためには、詳細な説明か、明確に定義された共通言語が必要となります。その共通言語の一つを「数学」で作ってしまった人がいます。京都大学の数学者、坂上貴之教授。「宇宙は数学の言葉で書かれている」とガリレオは言いましたが、坂上教授はどんな言葉を作り上げたのでしょう。

坂上貴之

京都大学 大学院 理学研究科 数学・数理解析専攻相関数理講座 教授
1998年 京都大学大学院理学研究科数学・数理解析専攻．1998年 名古屋大学大学院多元数理科学研究科助手．1999年京都大学博士（理学）を取得．2003年 北海道大学大学院理学研究院准(助)教授，その後同大学教授を経て，2013年より現職．
専門は数理流体力学・応用数学、流れに潜む豊かな数学的構造を明らかにすることで千変万化する流体運動の複雑さ・美しさを数学的に理解することに強い関心がある。また、流体数理の周辺諸分野への応用にも興味がある．
2002年日本数学会建部賞奨励賞、同年日本応用数理学会欧文誌論文賞、2019年現象数理学三村賞，2020年日本応用数理学会論文賞受賞

「流れ」のパターンを「言葉」にして共有する

「流れ」を「ことば」に……。それが、坂上教授が作り出したパターンに対する共通言語の表記法だ。「流れ」とは流体力学でいうところの、水や空気をはじめとする様々な流体の運動。目には見えない複雑な動きを続ける流れのパターンやかたちをひとつの数学的な言葉にしたのだ。

「専門は応用数学（非線形解析）です。中でも特に『流れ』を数学で記述する数理流体力学分野の研究をしています。元々、学生の頃から気象の話などが好きで、流体が好きだったんですよね。その複雑な動きを科学的に理解したいという思いが常にあり、理学部に入ったこともあって、複雑な流体の運動を理解するための学術として数学を専門に選びました」

　そして、応用数学研究者の道に進み、2007年、JST戦略的創造推進事業数学探索域（西浦廉政総括）の『さきがけ』と『CREST』で研究プロジェクトを推進、社会（企業）と連携して「様々な分野に数学を適用する研究」を開始した。

「社会との連携といっても、初めは右も左もわかりません。しかし、自分には流体力学に関する『理論』があるので、その『理論』を社会からのニーズを見ながら少しずつ実践的に応用していきました。そんな中で、企業の方々と話す機会も多く大変勉強になったわけですが、それによって気づいたのは『理解し合うための共通言語がない』ということでした」

　たとえば、共同研究を進めていく過程で、ある問題についてコンピュータシミュレーションを行なう。結果は画像データで出てくるのだが、その画像を見れば、相手も自分も「複雑だな。これはかなり難しいな」といったレベルの共通認識は持てる。いわば、直感的にあるいは情緒的に思いを共有できる。しかし、そこから論理的に詳細な議論を進めていこうとすると、対象を正確に捉えられる共通言語がない。だから、「ある対象をお互いがきちんと捉えられる言語体系がほしい」と思ったのが最初のきっかけだったそうだ。

「人間って、詳細なデータの細かい数字も含めてイメージするというよりも、ひとつの形、パターンとしてイメージしますよね。だから、『ざっくりとしたパターンを表現する言葉』があれば良いと思いました。数学にはトポロジーという分野がありますが、これはまさに形を大きく分類するために用いられる幾何学分野です。たとえば、コーヒーカップとドーナツは普通に見れば違う形をしていますが、トポロジーでは『穴がひとつ開いている同じ形』とみなします。コーヒーカップの取手部分とドーナツの穴は同じ『ひとつの穴』として考えるわけですね。この流体の画像のある部分の特徴をトポロジー的な描像として捉えれば、数学的な言葉（文字列）ができることがわかってきたのです」

　その時から、流れを表す数学的な言葉の理論を作り始め、数年で一定の完成を見た。そして、特許も取った。特許が取れたということは技術的に新しいということを意味している。また、この理論は学会から評価され、日本応用数理学会論文賞（応用部門）を受賞した。その後は現在に至るまで様々な分野の流体への適用を各分野の専門家と協働して進めている。

構造を表す名詞、COT表現

　では、坂上教授が作り出した「流れを表す言葉」とはどのようなものなのか。簡単な具体例を挙げて紹介しよう。

　たとえば、斜めに傾けた板を川の流れの中に置くとする。それを数値シミュレーションすると図 Aのような画像が出てくる。赤く細長い長方形が斜めに傾けた板、その上にある青や黒の曲線が水の流れがつくる渦（回転流領域）を表している。この画像から流線パターンを抽出すると、図Bのような図になる。そして、図Bの下にあるのが、この流れに与えられた「数学の言葉（文字列）」となる。ちなみに、t = 5.5というのはある時刻を表す。この時刻が5.5、6.6、7.7と経過するにつれ、流れの形も変化していく。

　坂上教授が作った数学の言葉（文字列）は「COT表現」という。COTとは、トポロジカルな構造に対して数学的に一意に割り当てられる「部分円順序根付き木表現（partially Cyclically Oredered rooted Tree representation）」という離散グラフのこと。このグラフを文字列として表現したものがCOT表現である。例えば、図A・Bのt = 5.5の時刻における流れパターンのCOT表現は、

COT表現　a_∅ (a₂ (λ+,c– (b_(–),{σ-,σ– },c_+ (σ+,λ-))))

になる。

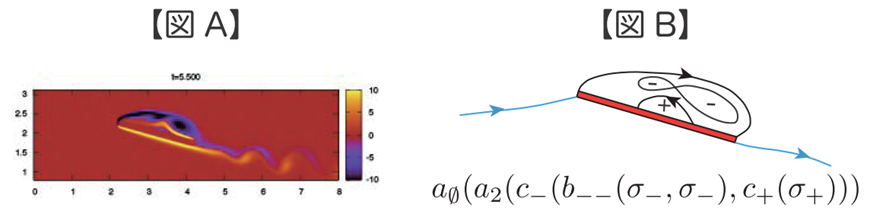
COT表現の最初にある「a_∅」 は、この流れが川の流れのような一様流の中にあることを表現している。その下にあるa₂ (λ+,c_ (…))「 」は「板の上に時計回りの流れを閉じ込めるような流れ構造」があることを示している。さらに、…の内部にある「b__,{σ-,σ– },c_+ (σ+,λ-)」の文字列はそれぞれ「8の字形の時計回りの流線構造」と「小さな反時計回りの流れを閉じ込める流線構造」があることを示している。つまり、この表現は「流れの構造がどんな要素の組み合わせになっているのか」を明示したひとつの単語になっているのだ。

　坂上教授の理論では、二次元の平面の上に縮まない（非圧縮な）流体の流れの作るパターンで、多少のノイズがあっても影響が受けないようなものについて、そのCOT表現の基本形は「a_∅ 」、「b_∅＋ 」、「 b_∅ｰ」の3種類しか存在せず、特徴的な流線構造は「a_± 」、「 a₂」、「b_±± 」、「b_±∓ 」、「c_± 」の5種類しかないことが数学的に厳密に示されている。つまり、計測や数値計算得られる流れはどんなものでも、そのほとんどがこの文字列の組み合わせで表現できるのである。

　COT表現は、パターンの意味と意味を合成してできた漢字のような「一見して意味の構造がわかる表意文字的な文字列」となっている。この「言葉」によって、込み入ったコミュニケーションが実現する。「ある大きな流れの中のこの部分とこの部分は……」という時、COT表現の文字列によってどこを指し示しているのかを特定できる。また、「この部分とこの部分はどちらも◯◯というパターンになっている」と言いたい時は、それに対応するCOT表現の文字列を使えばよいというわけだ。

データ処理を効率化し、分野をまたぐ共通言語

「この数学の言葉、COT表現によって流れに関する詳細な議論ができるようになりました。また、文字列化にはコミュニケーションが容易になるということだけでなく、様々な利点があります。いくつか挙げてみましょう。まず、膨大な数の画像データを文字列化することによって、大幅なデータ圧縮が可能となります。COT表現を用いたパターンのデータ解析を私達は『流線トポロジカルデータ解析』と呼んでいます。刻一刻と変化する流れを文字列の変化として記述するので、画像データ１枚が数十キロバイトだとすると、文字列データは数十バイト程度ですから1000分の1から10000分の1にデータ圧縮できます。さらに、文字列なのでコンピュータに実装しやすくなります。昨今はデータサイエンスが隆盛していますが、文字列化することによって効率的な流れデータ解析が可能になりますね。それから、この文字列化は『流れ』が関係する分野にはすべて適用できるルールなので分野をまたいだ共通言語になります。分野をまたぐので、各分野の専門家が培ってきた経験知や暗黙知を共通言語によって共有できることになるわけです」

　分野をまたぐ共通言語。現在のところ、どんな分野に適用されているのだろうか。

「過去には日本ニューマチック工業株式会社（NPK）さんと空気の流れによって、『粉体』をその粒度に応じて分離する機械の開発に関する共同研究を行いました。この流線トポロジカルデータ解析を応用した結果、従来よりも高い分離性能を持つ分級装置の開発に成功しました。シミュレーションで得られる空気の流れパターンを文字列化して解析していったのです。現在は医師の方々と心臓の左心室の中で起こる『血流』のパターンの流線トポロジカルデータ解析を推進しています。左心室の内部に発生する『渦流』と呼ばれる回転流領域の大きさやその心室内部における配置、およびそれらの一拍動における時間変化などを見る際に、文字列化によってパターンを認識するわけです。このように、『粉流』や『血流』をはじめ、文字列化は『流れ』があるものなら何にでも適用できます」

　流れがあるものなら何にでも適用できる数学の言葉なので、気象の「大気の流れ」、「海流」にも適用できるし、「電流」などにも適用できる。道路の渋滞を研究する渋滞学という分野があるが、そのような「クルマの流れ」、また、人が移動する「人流」にも適用できる可能性もあるそうだ。新型コロナ禍だった2020年頃に飛沫の動きを示した画像データがたくさん見られたが、その「飛沫の流れ」だって文字列化して数学の言葉にできるかもしれない。

「そしてもうひとつ。実際に様々な分野の専門家の方々と共同研究している過程で気づいたことがあります。それは『これまであまり注目していなかったけれど、自分達が達成したい目的に対して本質的に効いている流れのパターンに気づける』ということです。普通、私達は流れの画像を眺めた時に一番動きの大きいところ、一番変化しているところに目が行きがちです。これは専門家でもそうで、みんな、その部分が肝だと思って解析します。しかし、文字列化して解析していくと、その大きな変化に至る原因となる箇所が判明するのです。原因となる箇所は動きが小さくてあまり目を引きませんが、実はその部分が本質的に『効いていて』変化が起こるということですね」

　つまり、文字列化にすることによって、解析そのものが深化するのである。数学の言葉は様々な分野の知見の発展を促してくれる強力なツールとなるのだ。

数学の言葉のソフトウェア『psiclone』を開発

　様々な利点を持つ数学の言葉。これはもう、幅広い分野に適用して、学術的および技術的な発展を促していくべきであろう。つまり、広く社会実装することが世界に役立てるカギとなる。

「その通りですね。でも、幅広い分野の個別のケースにすべて数学者が関わって文字列化していくのは不可能です。数学的に困っている人と数学者の出会いの機会も限られていますしね。社会実装と呼ぶからには広く普及させる必要がありますが、そのためには、誰もが使える『解析したいデータを入力すれば数学の言葉に翻訳できるアプリケーションソフトウェア』の開発が必要となります。そこで、私達の研究グループではPythonを使って『psiclone（サイクロン）』という解析ソフトを開発しました」

　坂上教授が数学の言葉の理論を確立し、特許出願もしたが、それを実際に使ってもらうためには「その理論を実装したプログラム」が必要となった。ソフトウェアの開発は特許を活かすための必要条件なのだ。そこで、ソフトウェアを作ってくれる人や会社などを探したが、それはなかなか大変だったという。理論を理解して使いこなせる数学的知見を持っていて、なおかつソフトウェアを開発する技術を持っている人を探さなければならない。結果的に数学もソフトウェア開発もできる非常に優秀な若手の数学者に作ってもらった。

「今後、社会の課題に数学を大規模に役立てるためには『現代数学も分かるプログラマー』を養成していく必要があります。高い数学の知識を持ちながら職業としてソフトウェア開発者になる人材。つまり、ソフトウェアで数学と社会をつなぐ人ですね。現在、医師と共同研究している心臓の血流の解析は理論的に大きく拡張が行われていて、我々の『psiclone』を適用できないのです。『psiclone』は2次元の解析を行うツールですが、心室の中の血流を理解するには３次元での解析が必要ですから。そのため、現在のプロジェクトではこうした数学の知見を持ったプログラマーを擁する企業との共同開発を進めていて、ほぼ完成の域に到達しつつあります。社会実装まで本当もう少しのところまで来ているのでとても楽しみです」

　社会の様々な分野において数学の知見が必要となってきている現在、数学と社会をつなぐことがとても大切だ。ソフトウェアを作ることによって数学と社会のつながりを広げていくことができる。しかし、そもそも数学的に困っている人々が数学とつながるのはなかなか難しいことだろう。

「応用数学者の私としては社会に数学を役立てたいと考えています。そのために、以前から『諸分野のための数学よろず相談室（Math Clinic）』という活動をやっています。数学的に困っている人を患者に見立てて相談を受け、解決策を示したり、適した分野の数学者を紹介したり。いわば、数学分野の総合診療医のようなものですね。最初は京大理学部の分野横断の教育プログラムの一環としてやっていたのですが、最近ではJSTから支援を得て、同様のことをやっている全国の数学者にも助けをもらいながら、数学者集団による数学相談室のようになってきました」

　現在は応用数学者が数学相談を受けているわけだが、この数学相談を幅広く実施していくためには、数学者とは別に「数学と社会をつなぐ専門家」を養成していく必要がある。いわば、数学コーディネーターだ。「現代数学がわかるソフトウェア開発者」と「数学コーディネーター」。どちらも数学を社会に適用していくために欠かせない人材なのだ。

「社会と数学を本気でつなげようとすると、そうなってくるのですね。現代はひとつの技術が社会をがらりと変えてしまう時代ですから、数学ソフトウェア開発や数学コーディネートをビジネスにしてくれるアントレプレナーが出てくれば、社会は大きく変わっていくと思っています」

応用数学者が感じる「少し崩れたものの美」

　数学者は純粋数学者と応用数学者に大別されることがある。純粋数学者は数学という学問分野の中で完結した形での理論構築を目指していく。その完結した形は整然としていて、そこに「美」を感じる。一方、応用数学者は世界を数学で記述することを目指す。自然だけでなく、人為的なものも含めたすべてを数学で記述し、それによって世界を理解していく。いうなれば、純粋数学者は自己完結するアーティスト、応用数学者は社会と切り結ぶクリエイターだ。坂上教授の活動を見ていると、実際に新しい「数学の言葉」を生み出す創造性と社会にコミットする姿勢を併せ持つクリエイターに見えてくる。

「そんな応用数学者も数学に『美』は感じています。数学はきれいな形に当てはめて理解しようとする学問ですが、現実の世界はそのきれいな形から少し崩れた部分が必ずありますね。応用数学者はその崩れた部分も含めて『美』を感じているのだと思います。人が作るものも、完璧なシンメトリーの形に収めるより、どこかに『崩し』が入っているほうが魅力的に見えたりしますよね。それは『美』を感じているということだと思うのです」

　少し崩れたものにさえ美を感じる応用数学者が創った「数学の言葉」。やがて多くの人々の理解と共感を生み出していくことだろう。

文・清水修（ACADEMIC GROOVE MOVEMENT）